Featured Contents







Introduction
Based on our current research, we have strong evidence that the medal bonuses positively affect catch rates on the Pokemon GO Plus. We also have statistical evidence suggesting that the bonus provided by gold medals is 1.3; applied in a similar matter as other multipliers in the GUCT formula.
However, our current data are insufficient to determine empirically the bonus multipliers for bronze and silver medals. We hypothesize that bronze and silver medal bonuses are 1.1 and 1.2 respectively, but more data would be necessary before these can be reasonably confirmed.
Update: We were able to gather over 1000 new data points since the original study including 163 data points for the silver medal and 142 data points where the silver and gold medals were averaged. Our statistical tests with the new data failed to reject any of the multipliers we proposed.
Grand Unified Catch Theory
The Grand Unified Catch Theory can be stated as
$$Probability= 1- \left(1-\frac{BCR}{2*CPM} \right)^{Multipliers}$$
With Base Capture Rate dependent on Pokemon species and CPMultiplier dependent on Pokemon level. You can read more about BCR here and CPM here.
$$Multipliers=Ball*Curve*Berry*Throw*Medal $$Ball, Curve, Berry, Throw and Medal are set multipliers which are equal to 1 when not applied.
For more on the GUCT, click here!
The Medal Bonus
Our best predicted value for the gold medal bonus is 1.3.
So without any other bonuses, such as the case when using a Pokemon GO Plus, having a gold medal is equivalent to throwing 1.3 Poke Balls in each catch attempt.
We further hypothesize that bronze and silver medals in turn provide an 1.1 and 1.2 bonus, respectively.
| Medal | Pokemon Caught | Bonus |
|---|---|---|
Gold | 200 | 1.3 |
Silver | 50 | 1.2 |
Bronze | 10 | 1.1 |
| No Medal | 0 | 1 |
While the table above works for Pokemon with only one type, many Pokemon have two types. When Niantic announced the medals catch bonus, they stated, “If a Pokémon has multiple types, your bonus will be the average of your bonuses for each type.” So here is how the bonuses look for dual-type Pokemon if our hypothesis is correct:
| Medals | Gold | Silver | Bronze | No Medal |
| Gold | 1.30 | 1.25 | 1.20 | 1.15 |
| Silver | 1.25 | 1.20 | 1.15 | 1.10 |
| Bronze | 1.20 | 1.15 | 1.10 | 1.05 |
| No Medal | 1.15 | 1.10 | 1.05 | 1.00 |
The graph below shows much your catch rate can improve by Pokemon medals:
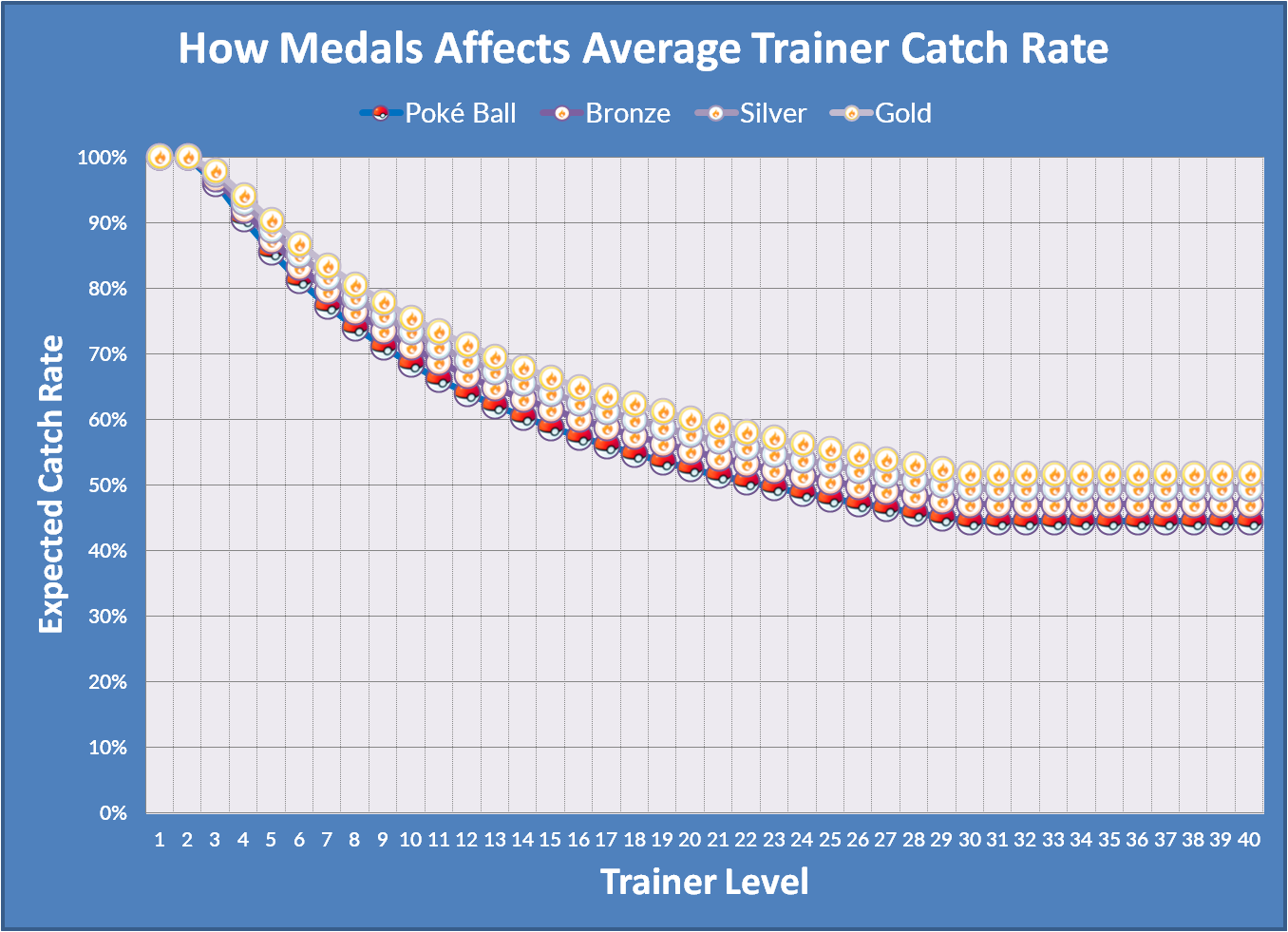
Click here to learn more about how we generated this graph.
Analysis
When the medal bonus was first announced, we went out and took screenshots of Pokemon and to see if we could estimate the amount of the bonus from the color of the capture ring. Unfortunately, we found that the color of the capture ring is not affected by medals. This result is in line with other research on reddit.
Because of this, we decided that the next easiest thing to do would be to hand collect data using the Pokemon GO Plus. This ensures that no other factors would contribute to the data, since the GO Plus only throws Poke Balls with no other multipliers. About half of the data points come from redditor /u/Spidertotz (thank you!), while the other half was collected by GamePress researchers. We have 1147 data points in total, 1053 of which are for the 3-medal bonus.
Before using this data to test the effect of medal bonuses, we first needed to verify that medals affect the catch rate of the Pokemon GO Plus. To do this, we calculated the expected catch rate using a Pokemon GO Plus prior to the medals update:
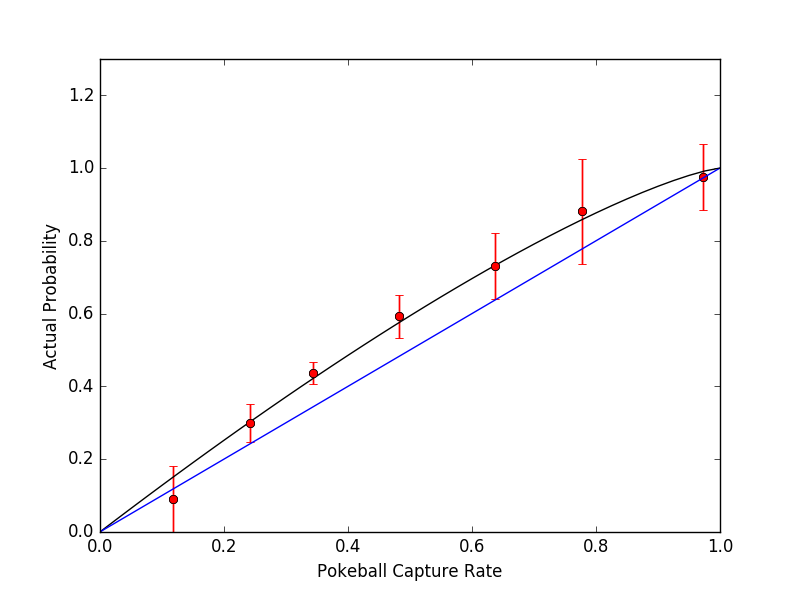
$$x=\frac{BCR}{2*CPM} $$Then, we restricted the data to only those where the 3-medal bonus applies. For all catch rates that had a sample over 15, we calculated the difference in the actual probability of capture and the predicted probability of capture without modifiers. As you can see from the scatter plot below, for most of the capture rates, the observed probability of capture was higher than the predicted probability.

To test if this was statistically significant, we ran a series of one tailed binomial tests. For 8 out of 29 of these tests, the observed probability of capture was statistically higher than the calculated rate without modifiers. This leads us to conclude that medal bonuses do in fact increase catch rate on the Pokemon GO Plus.
Once we established that the GO Plus data does indeed include medals, we tried to estimate the value of the gold medal multiplier. Our fitted data shows the gold medal multiplier as
$$Medal = 1.339 \pm 0.031$$
Like in the curveball analysis, the independent variable was chosen to be the simple Poke Ball capture rate, $$x=\frac{BCR}{2*CPM} $$
where x cannot exceed 1 (and is otherwise rounded down to 1).
1.3 is quite a reasonable guess for the actual bonus, which has always been a single-decimal number for the flat bonuses we've found in the past. Note that the +/- shows the 1-sigma interval caused by lack of sample size, so the actual number need not be in the interval. There is rounding error because our Poke Ball catch probability only had two decimal places, which is not incorporated into the graph or best fit value.
Let's see how this hypothesis fits the curve: if it is correct, the black line (GUCT theory with Medal = 1.3) should match with the red dots (actual catch percent for that bin) within error about 68% of the time, since the bars show one standard deviation = sqrt(nCatchSuccesses):
The graph is a nice fit. Admittedly, we first tried with 13 bins and the fit matched, but less nicely. With only 7 bins (above), the error due to sample size on each point / bin decreased enough that the fit looks good.
An obvious limitation of our study is the amount of data. Our second highest sample is 44, for the silver medal bonus, which is not enough to conduct rigorous statistical testing. However, there is one important theorem in math allows us to give a good hypothesis for the bronze and silver medal multipliers: There are only two whole numbers in between 0 and 3. So if the medal bonuses are single-decimal place numbers as the other bonuses have been, then they must be 1.1, 1.2, and 1.3, respectively. This is clearly just a reasonable theory, not a statistical conclusion, but we consider it likely enough that we'll go forth with those multipliers as we continue our research in this area.